Spell Balancing System in Wizard101

While everything in this article accurately models all of the spell changes that have been done, and the devs seem to have acknowledged its accuracy as much as they can without breaking some sort of company policy, this function is approximate and intended to capture the essence of how spell damage is determined. This was the first potential function I came up with, along with details of how I reverse engineered it, though I continue to come up with more possibilities based on comments the devs have given me (specifically, I know that the %acceleration isn’t quite right, and I know what the correct value is, which implies a slightly different type of function). Additionally, the more accurate functions I have come up with are based on the same model as this, more difficult to explain eloquently, and not significantly more accurate than this for spells below Rank 13 (i.e., you won’t need a closer approximation than this for any functional purpose), and therefore I decided to leave those out.

UPDATE: The actual function they use is a recursively defined function of Rank that outputs Spell Damage. While I now know what it is, the purpose of this article is more to show that there is a system for deciding damage, and this function is both an excellent approximation at reasonable Rank values, and defined as explicit (i.e., you can calculate a spell’s damage without knowing the damage of the rank before it), making it easier to calc specific spells.

Calculating Damage Per Pip

Now that the terminology is explained, I’ll start by going over how DPP is calculated. There’s a lot of misunderstanding about how DPP actually works, so hopefully this will clear some of that up. First of all: DPP is not constant, and never has been. DPP is calculated as an increasing function of Rank, meaning that DPP goes up as Rank does. The issue with finding the function itself is that limited knowledge is made public about the function’s form; looking at the values from the audit implies some sort of logarithmic or asymptotic function (think a curve that arcs upwards, and gets flatter and flatter as time goes on), but that’s as useful as that was. Fortunately, one of the developers, @Mattnetic, made a tweet that gave me enough information to infer the form of the function they use:

While this tweet is intentionally vague on its own, it pointed me in the right direction. Combining this tweet with the information I could infer from the audit, I had the following: Each school’s DPP curve is initialized with a different value that equates to their Rank 1 DPP (i.e., the DPP curve function has a constant value that is interchangeable based on which school you’re looking at). This value will be referred to as the Initialization Value and is the y-intercept on the physical graph of these curves. These values are, for the most part, what you’d expect when looking at the average damages of Rank 1 spells: 100 for Fire, 125 for Storm, 90 for Myth, and 85 for Death and Balance. Reverse engineering the equivalent value for Death drains gives 76. These, however, are the Standard DPP Curve values, and the Enhanced DPP Curves have different (read: higher) initialized values, which I will provide later.

Next, there’s some function of spell rank combined with this initialization, with some sort of constant %acceleration. Knowing the general curve of the function based on values in the audit, and based on Mattnetic’s tone in the above tweet, I concluded that for each Rank a spell increases, Spell Damage increases by a percentage of the initialized curve value, i.e., by a flat percentage of a school’s Rank 1 DPP. At this point, I had assumed each school had a different %acceleration value.

The one issue here is for Ice and Life: when trying to figure out what the DPP curve function was, the last little hint was that the %acceleration was the same between each school’s DPP curve. This implied that Ice and Life were initialized at 83 based on the numbers I had come up with. Otherwise, using the same %acceleration value for all curves would lead to Ice/Life having the exact same curve as Death/Balance, given their Rank 1 spells deal the same average damage.

In essence, you could think of Frost Beetle and Imp being rounded up to 85 average damage from the 83 damage that they would do based on the function. This suspicion was confirmed the day after I figured out the function by the official Wizard101Devs twitter account. This gave me a %acceleration value of 13% (I now know this value is slightly off from what the devs meant, but when using this version of the function provides the most accurate results, enough so to reverse engineer the following curve initializations correctly).

After knowing what the function looked like, I reverse engineered the initialized values for the Enhanced DPP Tracks, those being: 130 for Storm, 120 for Fire, 115 for Myth, 105 for Death/Balance, 100 for Ice/Life, and 95 for Death drains (EDIT: While writing, these initialization numbers, along with those for the Standard Curves, were officially confirmed via the Spell Balance Audit developer diary on the Wizard101 website). Additionally, there isn’t a lot of data on Shadow damage spells, but Dark Nova and Fiend are on a curve initialized at 150 (Fiend is slightly above the curve), and Shepherd on a curve initialized at slightly above 135.

Damage Per Pip Functions

As for what the function looks like: the concept, again, is that the Spell Damage at a given rank is given by taking the rank value of the spell, multiplying by the school’s initialized value (i.e., the Rank 1 DPP), and adding 13% of the school’s initialized DPP for each rank value above 1. Therefore, letting A be the initialized DPP value of a school, and letting R be the rank of the spell, I found the following:

Spell Damage=A*(R+0.13*(R-1))

From here, you divide the whole thing by R to get the DPP value. Hence:

DPP=(A*(R+0.13*(R-1)))/R

Here’s a graph of this function, with the proper initialization values (y-intercept) for each school: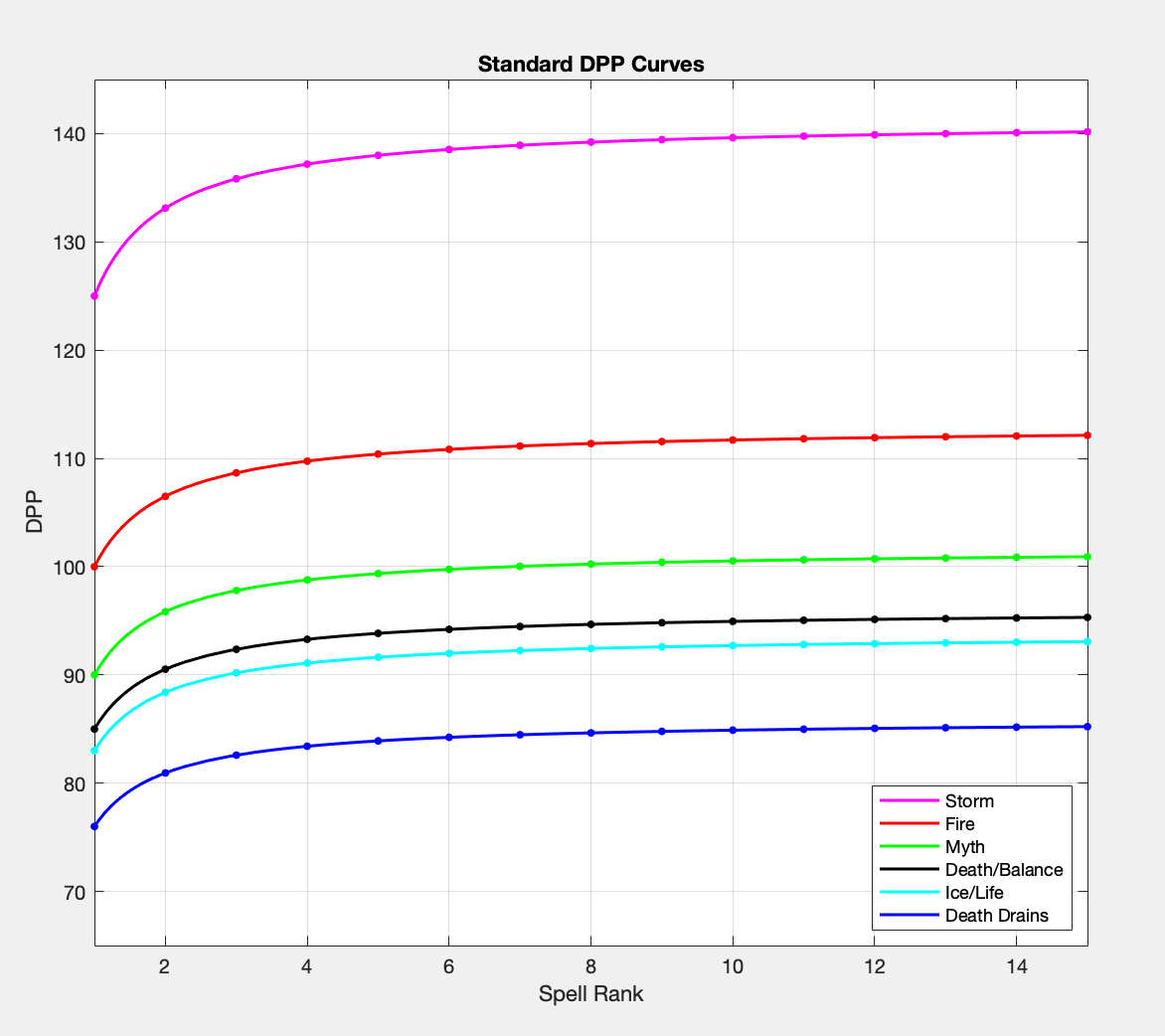

Additionally, here’s a graph of the Enhanced DPP Curves based on this function:

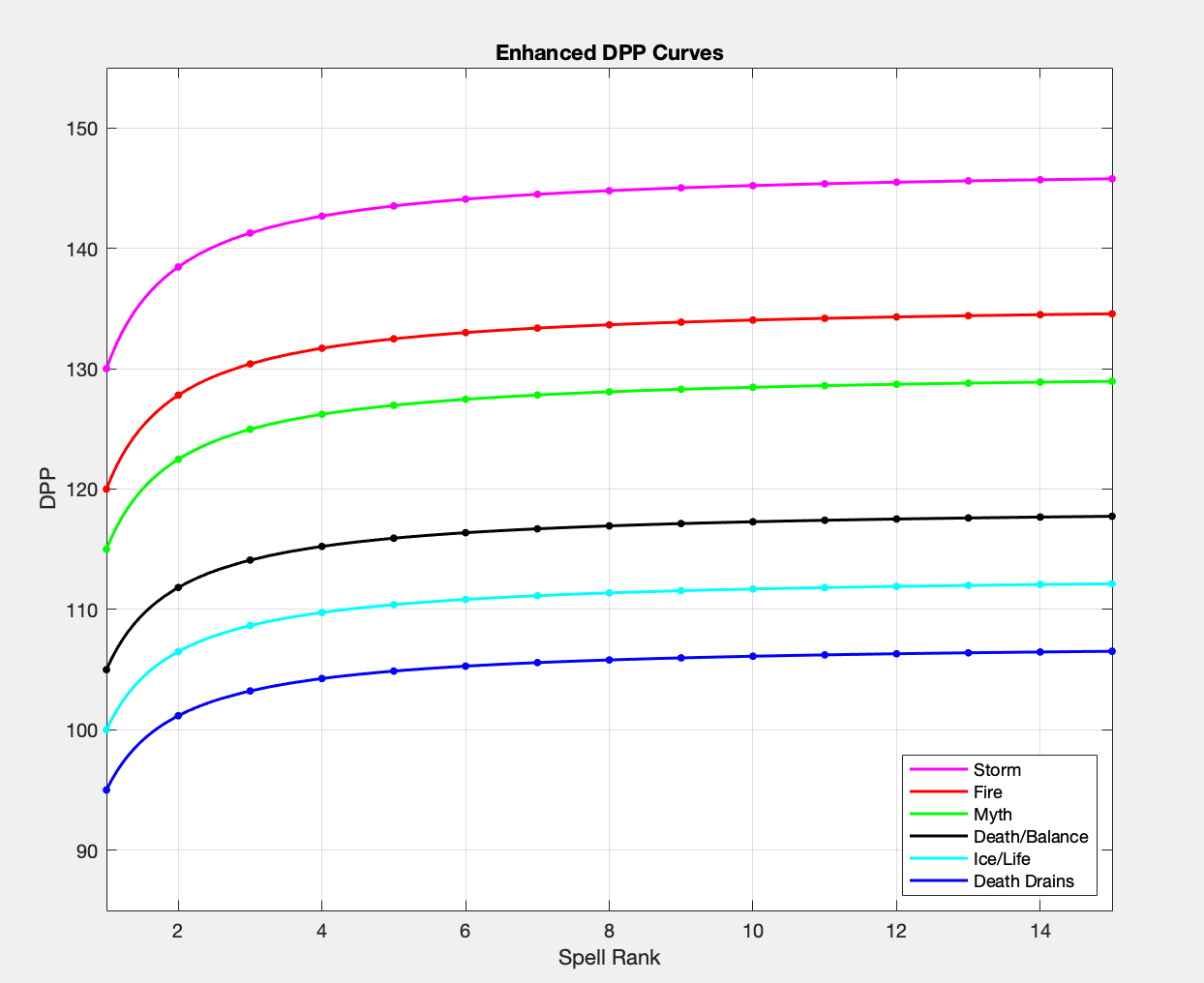
Note that the school curves are spaced much more evenly on the second graph, which was the intention when raising each school’s Curve Initialization (y-intercept) for the Enhanced Curves. There is also virtually no visible difference on a graph of this scale between the function explained above and more accurate versions I have come up with since.

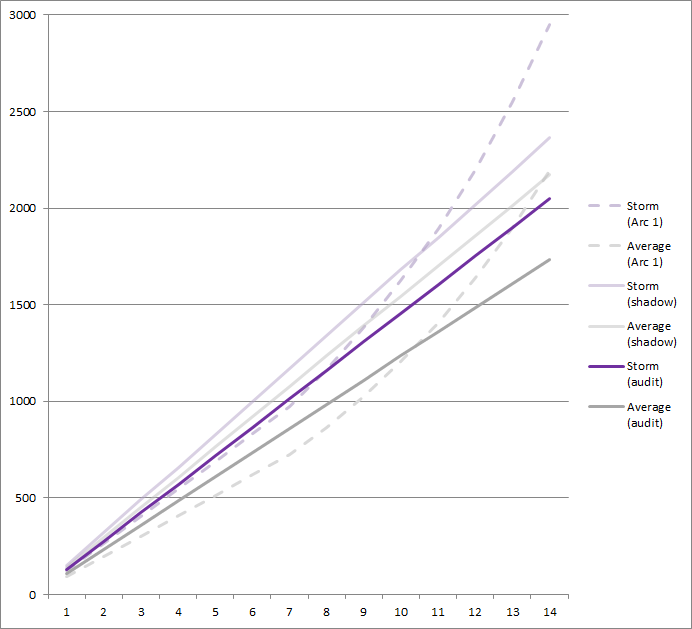
Anyone sufficiently familiar with mathematics should recognize this function as being asymptotic, or approaching a line as Rank increases to infinity. The implication here is that Spell Damage approaches a linear function (or something like it) of Rank as Rank gets larger. The Wizard101 devs, as shown through a graph that their official Twitter account shared with me and later posted in their developer diary post (below), intend to make this change from the standard set by the original devs in 2007, which was having Spell Damage being closer to a function with an exponential element, or a hockey stick graph (there was an extra DPP accelerator in the function), which caused the power disparity between the schools (most notably, Storm) to grow unreasonably as Rank increased.

An Example

To practice, let’s calculate Ice’s Standard DPP at Rank 5. First, we note the initialized value for Ice/Life, that being 83. Then, for Rank 5, we take 83*(5+0.13*(5-1))=83*(5.52)=458.16. Finally, we divide by 5 one last time, giving 91.632 DPP for Ice at Rank 5. In this case, the Standard DPP Rank 5 spell for Ice would be Frostbite. Frostbite is a DoT, so it gets a 25% total damage boost (more on damage modifiers later), and has no side effect, meaning to be on curve, Frostbite would have to do 91.632*5*1.25=572.7 total damage. Before the audit, Frostbite did 70+480 DoT, or 550 total damage, which put it below the curve; however, we can see the audit work its magic, as Frostbite was buffed to do 80+495 DoT, or 575 total damage, putting it perfectly in line with the curve. You can expect other old spells to be buffed as the devs continue the audit.

One last bit on DPP: the reason the DPP function was so confusing to pinpoint was largely because the devs have artistic freedom to tweak damage values, and for the vast majority of spells that at least means rounding to the nearest multiple of 5 (if there’s a specific reason not to, such as some effect on the spell, then they’ll round differently; for the 4-pip shadow-enhanced spells, for example, they round to the nearest multiple of 12 in order to be able to divide the damage by 2, 3, and 4 when necessary). Sometimes, they’ll push values even more than that based on what feels right functionally, without breaking the curve.

Tempo/Utility Cost

“Wait, is that all there is to it?” Though DPP is a huge part of spell balancing, and was essentially the last piece of the puzzle to figure out, it isn’t all that goes into spell balancing. The next step, after calculating a spell’s DPP, is for the devs to figure out how many Ranks of the spell should go towards damage, and how many Ranks should go towards tempo and utility value. Tempo and utility deductions are currently based on a fairly straightforward set of rules (though a few spells exist that work at the theoretical edge of the system, so to speak).

First, if a spell has a secondary effect, that itself is valued at one Rank because of the tempo saved by doing two things in one round. Second, if the effect is an AoE (i.e., it is applied to all opponents or all allies), an additional one Rank of value is given to tempo/utility. Next, the rank value of the utility itself also goes towards tempo/utility cost. If a Rank 0 utility is added, no additional Ranks go to tempo/utility, if a Rank 1 utility is added, one additional Rank goes to tempo/utility, and so on. Finally, once they know how many ranks of the total value of the spell go towards tempo/utility, if the PIP COST (NOT Rank value) of the spell is 8 or above, the amount of Ranks that go towards tempo/utility is cut in half. This is to compensate for forcing a high-value spell to have a secondary effect that in some situations is of limited value.

An Example

Now that we know how many Rank values go towards tempo/utility, we can calculate the unadjusted damage of the spell by subtracting the Rank value that goes towards tempo/rank by the total Rank value of the spell.

For example, take Dr. Von’s Monster: the Death drain DPP curve puts a Rank 9 Death drain at 84.782 DPP. Dr. Von’s Monster has a utility added, so that puts 1 Rank value towards tempo/utility. That utility is single target, so we DON’T put another Rank value towards tempo/utility for that reason. The utility’s value (i.e., the Rank value of a 50% infection) is 0, so no more Rank values need to be put towards tempo/utility. Finally, since the spell costs 8 or more pips to cast (it costs 9), we divide the number of ranks that go towards tempo/utility by 2: 1/2=0.5 Ranks of value reserved for tempo/utility.

This implies that 8.5 Ranks go to the damage of Dr. Von’s Monster. Referencing the Rank 9 Drain DPP of 84.782 (see the above section), we multiply 84.782*8.5=720.65, giving 720 for the expected damage value of the spell (at the time of writing, Dr. Von’s Monster is incorrectly using Death’s flat damage DPP curve instead of the drain curve, resulting in 810 damage, a mistake the devs have acknowledged and rectified)

Valuing Unprecedented Utilities

Now that we’ve talked about the amount of Rank value that goes to tempo/utility, it’s worth talking about the Rank valuation of utilities themselves. This is the most subjective part of the balancing process, and is where the devs could use the most feedback when balancing spells. If there’s a spell already in the game that is a utility-only spell and equivalent to the added utility effect on the spell they’re balancing, the rank valuation is pretty clear-cut. For example, a 25% weakness, 50% universal shield, and stun one target effect added to a damage spell all pretty clearly value at 0 Ranks. Additionally, a dispel would clearly value at 2 Ranks, and, in the current pre-audit state, a Shatter or Enfeeble would value at 3 Ranks (this could change based on how the audit treats infinite removal spells; the idea is that spells that are strictly utility set a precedent for utility valuation).

How, though, do you treat a 45% weakness? Or a 75% Tower Shield? Or a “remove 2 positive charms” effect? This has to do with saved tempo and diminishing returns. Saved tempo, in simple terms, refers to how many rounds you save when using an effect compared to similar ones in the game.

An Example

For example: to create the effect of a 75% Tower Shield, you would need to spend two rounds stacking 50% Tower Shields, based on existing trainable spells in the game. Therefore, applying a 75% Tower Shield saves 1 round over using two Rank 0 utilities; saving 1 round of tempo, as discussed in the previous section, is worth 1 Rank of value. Therefore, a 75% Tower Shield would be worth 1 Rank.

Similarly, a 1 Rank Weakness would value at 45% (the derivation of these values is trivial and left as an exercise for the reader). For double Disarm: as of the time of writing, Disarm is valued at 1 Rank, but the devs have essentially confirmed that Disarm should value at 0 Ranks in line with Pierce, Cleanse Charm, and Cleanse Ward, and will likely change when audited. With this in mind, a double Disarm would also value at 1 Rank.

Diminishing Returns

Diminishing returns is exactly what it sounds like: the more saved tempo you get from an effect, the less valuable each additional saved tempo is. For instance, saving 5 tempos vs 4 tempos is much less valuable than saving 2 tempos vs 1 tempo. This is where some subjectivity comes in: How strong does the diminishing return effect get for different utilities, and how quickly does it start to take effect? For most effects, though, I would say the effect shouldn’t take hold until at least 2 saved tempos. Since most current spells don’t have any secondary utility effects that have more than 1 saved tempo, the diminishing returns effect rarely comes into play in this context.

It is, however, a theoretical concept that is important to acknowledge. If there were no diminishing return effect, theoretically, based on the above paragraph, a 100% Tower Shield should be worth infinite Rank values. Logically, however, this isn’t the case at all; therefore, the diminishing returns effect is fairly intuitive.

Damage modifiers are boosts or reductions given to the damage of a spell after their damage has been calculated when adjusting for DPP and utility. The damage modifiers we currently know of are the following:

• DoT spells: 25% boost to total damage
• AoE spells: 25% reduction to total damage
• X-pip spells: 15-25% reduction to total damage (the devs have implied that they haven’t decided what the reduction will be)

The reason DoT spells get a boost is to compensate for the inconvenience of having to wait for damage to be dealt. The devs have freedom to shift damage to the initial and DoT portion of the spell. The reason AoE spells get a reduction is to compensate for the luxury of targeting all combatants on one side of the duel circle. The reason X-pip spells will be getting a reduction is to compensate for the flexibility of being able to cast them at any time.

More on X-pip spells: the original balancing of Tempest, and the recent rebalancing of Snowball Barrage, already take some sort of devaluation into account. Heckhound and Judgement are the other two main spells that would be affected by this reduction during an audit. The argument “The spells force you to lose all your pips, that’s enough of a drawback!” doesn’t refute an X-pip devaluation. Converting all of your pips to damage is the only effect of the spell; that’s why you use it. You have the luxury of not having to use them if you don’t want to use all of your pips, and to instead choose a different spell that uses the exact number of pips that you’re willing to lose.

X-pip spells are effectively 14 spells in one, and that’s the reason we should be paying a price for them. From what Mattnetic specifically has said, the exact % devaluation of X-pip spells is debatable, and probably will change based on school (i.e., the X-pip devaluation is likely going to be more subjective than the DoT and AoE modifiers)

Shadow and Shadow-Enhanced Spells

For shadow-enhanced spells, the first thing to note is that you can’t think of rank value as pip cost like you can with regular spells; this is why I’ve avoided using the two terms interchangeably. The Rank value of a single shadow pip, as of now, is 3.6. This means that the Rank value of any spell involving a shadow pip is their regular pip cost plus their shadow pip cost multiplied by 3.6. This applies to shadow-enhanced spells, as well as shadow transformations and shadow creatures.

With this in mind, shadow transformations have a total Rank value of 3.6, shadow creatures have a total Rank value of 7.2, and 4, 5, and 6 pip shadow-enhanced spells have a total Rank value of 7.6, 8.6, and 9.6, respectively. Shadow transformations are incredibly high Rank value utilities with several drawbacks, and don’t really set precedents for other spells. Shadow creatures can be thought of as Shadow school attacks on a Shadow DPP curve, but we only have data for 3 points: two for a flat Shadow damage curve (Rank 7.2 DPP=166.67 for Nova, 169.44 for Fiend), and one on the Shadow drain curve (Rank 7.2 DPP=150.93).

Finally, shadow-enhanced spells. These spells fall into each school’s Enhanced DPP Curve, with the input of the DPP Curve function being their total Rank value (NOT their pip cost). The calculations from there are exactly the same as with the Standard DPP Curves. To finish off this section, I’ll provide an example by verifying that Abominable Weaver is balanced under this system.

An Example

Abominable Weaver has a total Rank value of 8.6, with an added utility of a 50% Tower Shield. For saving a round by having an effect, 1 Rank value goes towards tempo/utility. Since the effect is not AoE and has Rank value 0, no more Rank values need to go towards tempo/utility. Then, Ice’s Enhanced DPP Curve puts Rank 8.6 Enhanced Ice DPP at 111.49. Since 1 Rank goes to tempo/utility, that leaves 7.6 Ranks to go towards damage. Finally, 7.6 Ranks multiplied by 111.49 DPP gives 847.31 damage. The spell does 790-910 damage, so we can see that the devs rounded up to give it an average of 850 damage.

Scions

The Scion spells are interesting. What they do as of the time of writing is value the damage doubling condition as a Rank 1 utility. This means that 2 Ranks of value go towards tempo/utility, which gets cut in half since their pip cost is 8 or higher. So, they each have 10 Ranks of damage value at their respective school’s Rank 11 DPP. Despite having -5% accuracy, which usually denotes an Enhanced DPP spell, these spells are evaluated using Standard DPP.

Sun Serpent/Avenging Fossil

These spells value the secondary damage hit as a utility, and value said utility by looking at the Rank value of the damage dealt. The secondary hit of Sun Serpent is worth 4 Ranks of DPP, and the secondary hit of Avenging Fossil is worth 3 Ranks of DPP. Since both spells cost 8 pips or more, the total Rank value for tempo/utility is 2.5 for Sun Serpent, and 2 for Avenging Fossil, meaning Sun Serpent gets 7.5 Ranks of damage and Avenging Fossil gets 8 Ranks of damage on their initial hits.

Rank 7 AoEs

The Rank 7 AoEs are all intentionally balanced as single-target attacks, i.e., the AoE damage modifier is not applied to them. Otherwise, they’re exactly on their respective DPP curves. They were balanced over the curve because that’s what players seemed to want.

King Artorius

The school spear effects were given out for free. This is reasonable since all schools get the effect, and the functional value is so low that there isn’t a hugely noticeable power increase over other spells, but it’s a debatable issue. I see no issue with it.

Hydra / Chimera / Spectral Blast / Nested Fury

These spells’ DPP are based on the school of the damage it deals, not based on the school of the spell itself. For Spectral Blast and Nested Fury, that means basing their damage off of the individual Elemental schools’ DPP curves. For blended spells like Hydra and Chimera, the devs have said that the intent is to use the DPP function initialized at the average of the blended schools’ initializations (i.e., the average of Elemental and Spirit initializations for Hydra and Chimera, respectively). As of the time of writing, both Hydra and Chimera use a curve based on the average of Elemental initializations, which could be intentional to make Chimera feel like a sufficient upgrade from Hydra (if Chimera used the Spirit initialization, it would be at 290 per hit).

Gaze of Fate

Like Balance’s other spells that hit with non-Balance damage, Gaze of Fate makes use of an “average” DPP Curve for the part that hits with off-school damage. Namely, the off-school curve is initialized at 111.67, i.e., the average of the Enhanced Curve initializations for the other 6 schools. The global damage boost is valued at Rank 2, in line with other global spells, and after taking away 1 more Rank for tempo, that leaves Gaze of Fate with 5.6 Ranks of damage, which is split evenly at 2.8 Ranks for the Balance damage, and 2.8 Ranks for the off-school damage.

Four-Pip Shadow-Enhanced Spells

These spells value the ability to split damage as a Rank 0 utility. Knowing this, they’re correctly balanced on their respective Enhanced DPP Curves, rounded to the nearest multiple of 12 to make sure it’s possible to split damage to 2, 3, and 4 targets.

Rusalka’s Wrath

This is the only spell that has been audited that has a negative utility attached. As you could probably guess, the negative utility adds damage value. First, to explain how my terminology would treat this, I would say that both a blade and weakness on yourself would value as Rank 0 utilities, but the blade would add 1 Rank of tempo, while the weakness would subtract 1 Rank of tempo. Therefore, a 100% chance of a blade should put a total of 1 Rank towards tempo/utility, while a 100% chance of a weakness should put a total of -1 Ranks towards tempo/utility. Since the odds for Rusalka’s Wrath are somewhere between those two options, tempo/utility gets somewhere between -1 and 1 Rank. Working backwards, based on the function I have here, the spell puts 0.3 Ranks towards tempo/utility, implying that there is something like a 65% to get a blade, and a 35% chance to get a weakness (assuming they value a 30% blade vs a 30% weakness equally. However, they might have valued the 30% weakness as stronger, since multiplicatively it’s more valuable).

Snowball Barrage

Mathematically, this spell is balanced as it was in one of its test realm builds, with a +250 gargantuan-like damage addition to account for the value of a shadow pip. The devs thought that contextually, that made Snowball Barrage too powerful at low pip values, and instead added per pip damage to compensate for the shadow pip’s value. Some sort of X-pip damage reduction is also taken into account.

Heals

Heal DPP is something I’ve left out of this article, because it’s frankly all over the place as it is now. Presumably, heal DPP will follow the same function archetype and have the same %acceleration, and the heal DPP curve will differ by school, with Life’s being the strongest. However, there isn’t a lot of information right now. There are only 4 healing spells recent enough to be under the new system (i.e., that would give accurate current data about the curves): Wings of Fate, Rebirth, Scion of Life, and Grendel’s Amends.

For Wings of Fate, the first issue is that it’s a shadow-enhanced spell, which likely implies a different healing DPP Curve from the others, and the second issue is that I can’t be sure how they value splitting Rank value into damage and healing as a utility. For Rebirth, I’m not sure how they value the AoE Spirit Armor effect, so I can’t initialize its curve accurately. Then, there’s Scion of Life, which I can pretty confidently put on a curve initialized at around 168 DPP. On this curve for Life heal DPP, Rebirth would be valuing a Spirit Armor effect at 1.5 Ranks (already factoring in the value being cut in half for Rebirth being 8 pips or above), which makes qualitative sense and would imply auditing Spirit Armor to be a 2 pip spell. Knowing the standard Life heal DPP initialization, my best guess for the Life heal Enhanced DPP initialization would be 180, which would imply the devs value the effect of splitting Wings of Fate into damage and heal as a Rank 0 effect, and that the Rank value of the spell gives 4.3 Ranks of damage and 4.3 Ranks of healing (perfectly balanced!).

Grendel’s Amends has the same issue as Wings of Fate in that there’s only one data point that would be on its presumable curve. The current value would put the Myth heal Enhanced DPP initialization at 122.5, which seems reasonable given the values for Life heal DPP I’ve conjectured.

However, this isn’t really much to go off of. The full audit will tell exactly how heals are being evaluated, in terms of curve initialization. I would be confident enough to project what a heal audit would look like based on this, but that’s probably a topic for another article.

“It’s not all math. Pure math doesn’t make good game design.”

While true, the point of the spell audit is that spells need to be initially brought to a standard that is able to support the growth of the game, then adjusted in context. The mathematical curve that spells were on before was one that grows increasingly quickly as Rank increases. This does not bode well for the long-term health of the game because it accelerates power creep. Once the devs bring spells down to the new standard, which is undeniably better for the long-term health of the game, the relative mathematical value and functional sensibility of effects can be debated, considered, and changed. However, it needs to be taken one step at a time.

“Why is there a DPP accelerator at all?”

A DPP accelerator is necessary to make sure that each subsequent spell we gain is stronger than the last, and perhaps more importantly, to make sure that each pip gained in combat is more valuable than the last. It exists to make the pacing of combat feel more strategic and rewarding by rewarding players for being decisive with their actions.

“You can’t have a spell that’s worth half a pip. Why could [insert utility here] only be valued at a decimal Rank value?”

This goes back to the distinction between Rank and pip cost. Sure, a spell can’t cost half a pip, but based on existing precedents and some subjectivity, we can Rank value certain utilities to have decimal Rank values. All shadow spells, for example, have a decimal Rank value. Another example, how would you value a 65% Tower Shield? Multiplicatively, half of a 50% Tower Shield is a 30% Tower Shield (i.e., stacking two 30% Tower Shield gives roughly the same reduction as a 50% Tower Shield). Further, stacking a 50% with a 30% Tower Shield brings the total reduction to 65%. Therefore, a 65% Tower Shield is halfway between a 50% Tower Shield, and stacking two 50% Tower Shields in terms of Rank value, and so should be valued at 0.5 Ranks. Logically, the sense of this is that if you have two spells with identical damage, but one has a slightly stronger effect in a way that has no valuing precedent (like a 50% vs 65% shield), it doesn’t make sense to value them equally; the slightly stronger effect should have slightly less damage.

“Why were the spells tinkered with so much if there’s a clear formula for calculating what spell damage should be?”

Like I said earlier, it’s not all math. The devs change the balancing rules and some spell design based on what is contextually logical. The 5 pip shadow-enhanced spells, for example, were originally on the Standard DPP Curves, but were changed to be on the Enhanced DPP Curves, hence the buffs from the initial balancing.

Additionally, the rule of halving the tempo/utility value for secondary effects on spells with a pip cost of 8 or higher was a new standard the devs implemented in the middle of the most recent test realm, hence the buff to most spells costing 8 pips or more (this was done because it’s a drawback for a high value spell to be forced to have some of it’s value put into a situational effect, so they get compensated for it. You don’t have the luxury of forgoing the side effect in situations where it isn’t needed, but still need the spell for the high damage value, hence the compensation). If you’re able to get a good grasp on their balancing system, it’s easy to track the devs’ thought processes while balancing, which is both fascinating for its own sake, and useful as a baseline for giving constructive feedback.

“If this is the new function, what was the old one?”

I’m not exactly sure about this one, mostly because I haven’t looked into it too much. The current devs themselves haven’t either; they didn’t have to. What they did was remove an accelerator that was added to spells at Rank 8 and above. It was such a clear problem in terms of causing damage to skyrocket at higher ranks that they didn’t even need to look into exactly what it did before deciding to remove it. What seems to be the case would be that it multiplied the total damage of a spell by something like 1.05 for each Rank above 7, which adds an exponential component to the Curves above Rank 8, creating a hockey stick shape in the graph of Spell Damage against Rank. Regardless of the exact numbers of this extra accelerator, as lead designer Ratbeard eloquently put, “it was bonkers.”

“[Insert spell here] seems overpowered/underpowered! What happened?”

This is probably due to how the devs valued a specific effect, which could differ from your expectation. The devs have to balance for all parts of the game, meaning that if you focus on one specific area (most notably, PvP vs PvE), you might find that some spell effects were made to cost differently than you would subjectively value them as. For example, they valued the minion summoning effect of Witch’s House Call as a Rank 0 utility (because it’s useless with a full team in PvE), the “opponent loses 2 pips” effect of Lord of Winter as a Rank 0 utility, and the pip stealing effect of Celestial Calendar as a Rank 0 utility. I would encourage discussion regarding effect value of any spell with the devs via their official Twitter, though keep in mind that they DID follow a system and have a reason for putting a spell where it is. They don’t rebalance spells arbitrarily.

“What’s up with DoTs? Do they apply the damage boost to the initial hit too? Isn’t that an issue?”

The devs’ treatment of DoT spells could be considered mathematically flawed, but functionally will not cause issues if they keep an eye on it. By applying the 25% damage boost to the total damage rather than only the DoT portion, they can create a problem if DoT spells are made too front-loaded. If the devs create a spell where 80% or more of the total damage is in the initial portion, the initial hit of said DoT spell will be as strong or stronger than a flat damage spell of the same Rank value, which nullifies the theoretical disadvantage of a DoT spell and therefore the reason for the 25% damage boost in the first place. As an example, a Rank 9 Fire non-DoT AoE spell on Standard DPP would be expected to do 755 damage (rounded to the nearest multiple of 5). However, Rain of Fire’s total damage is (and should be) 940. Since the devs have the liberty to shift damage to and from the initial and DoT portions of the spell, they could theoretically make Rain of Fire do 755+185 DoT damage, which would have the same exact effect and benefits of the flat damage valued at the same Rank, but get a 185 DoT for free on the end.

The solution the devs have come up with here is that they will be careful when front-loading DoTs, and will make sure they have a reason for doing so if they do it. I think this is reasonable, as we don’t have many DoTs in the game that have anywhere close to the dangerous 80% of total damage in the initial hit; the closest is Fire Dragon, which at the time of writing has 55% in the initial hit. Contextually, you might say that the system being reasonable is that damage enchants will split their damage between the initial and DoT portions; however, although it mitigates the theoretical issue, it only pushes it further into the distance (the “danger number” will still exist, and it will depend on how strong the current best enchantment is as well as the total damage of the DoT being looked at), and damage spells should not need to take enchantments into account when being balanced.

“What’s the DPP of an X-pip spell?”

This is something that we don’t know yet, since the only X-pip spell that has been audited is Snowball Barrage, which is a very unique case. What we DO know is that there will be a damage reduction given to X-pip spells.